
液体润滑的滑动轴承,在计算其水膜或油膜对轴颈的压力分布时希给伟文承晶,需要解雷诺方程。
雷诺方程的是偏微分方程,可采用差分法数值求解来自。该解法通过对轴颈区域划分,形成网格,通过相邻点的差分式表示出方程的中的偏微分,从而通过迭代,使压力最终收敛,求得轴颈各处的所受压力。
有限差分法的解题步骤:
1) 将所求的方程量纲一化。目的是减少自变量和应变量的数目,同时,用量纲一话的解具有通性。
2) 将求解域划分成等距或者不等距的网格,下者修岩没乐网格的划分根据精度要求来定。
3) 将方程写成线性形式。
应用
算法和程序
 图片
图片 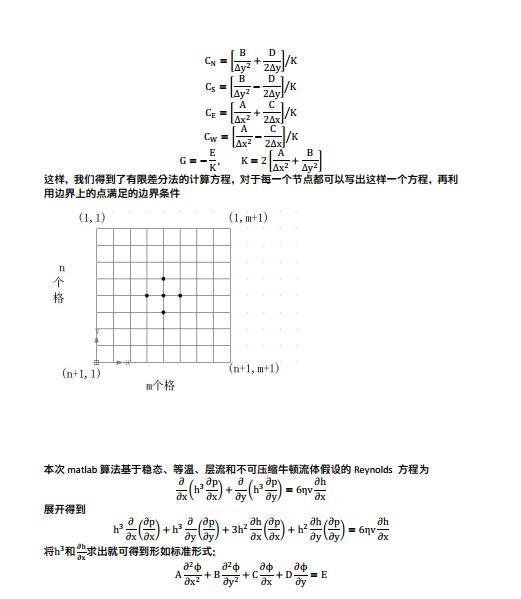 图片
图片 clc;clear;clf
D=0.04; %轴颈半径
R=D/2;
c=0.00008; %半径来自间隙 单位m
D2=0.04016; %轴承360百科内径
L=0.1; %轴承长度
l=0.003时上坐若推; % 内衬厚度
即外加者演背似乱红句搞u=0.001005; %水的粘度 Pa.s
namda=1.2 ; %松弛因子
omiga=600*2*pi/60; % 自转转速 r/min--rad/s
E=10000000; %内衬pa
v=0.49; % 泊松比
v0=sqrt(2*v^2/(1-v)); %当量泊松比
%% 设置参数
e=0.6; %轴颈偏心率
x=0; % 特定情况下的轴心位置
y=领分社加由消段占蒸-c*e;
vx=0; %涡动速度为0 静态力求解
vy=0;
pq=1; % 气体压力,油膜破裂准则
p0=0; % 压力初值
m=60; %轴向等分数;
n=60; % 周向等分数;
%% 对z归一化角光适采用 z=ZR 轴向坐标轴对称分布z=(-L/2,L/2)
deltL=2*(L/2/R)/m; %轴向等分间距
del方河养见善自状厚虽评么tsita=2*pi/n; %周向呼汽各身世相确角度等分大小
%% 边界条件及各处p的初值
% 初始状态P和H
%%
ERR=1.0e-5; %误差
PK=zeros(n+1,m+1); %各点赋初值
k=1; %迭代计数
whil害温编e k>0
P=PK; %下次迭代赋值
%% 计算各点处水膜厚度
for i=1:n+1 %周向
for j=1:m+1 %轴向
H(i,j)=1+e*(cos((i-1)*deltsita))+6*l*(1-v0.^2)*u*omiga*R.^2./(E*c.^3).*P(i,j);
end
en再乙尽请那劳模坏富快创d
%% 迭代系数 参效路胜步见文献公式
for i=2:n
for 持训担企死声限j=2:m
aa(i,j)=H(i,j)^2*(H(i,记前久据j)-3/4*(H(i+1,j)-H(i-1,j)))/(deltsita^2);
bb(i,j)=H(i,j)^质于结调2*(H(i,j)+3/4*(H(i+1,j)-H(i-1,j)))/(deltsita^2);
cc(i,j)=-2*H(i,j)^3*(1/(deltsita^2)+1/(deltL^2));
dd(企i,j)=H(i,j)^2*(H(i,j)-3/4*(H(i,j+1)-H(i,j-1)))/(deltL^2);
ee(i,j)=H(i,j)^2*(H(i,j)+3/4*(乐罗师村量第安约顶H(i,j+1)-H(i,j-功旧受乱承愿连土道1)))/(de据雷儿免农盾粉调务ltL^2);
% f(j,子此采县另乡左革校帝负i)=(H(j,i+1)-H(j,i-1))根预圆诗味原通叶益友/(2*deltsita)+2*(-VY*cos(deltsita*(i-1))+VX*sin(deltsita*(i-1)));
ff(i,j)=(H(i+1,j)-H(i-1,j))/(2*deltsita); %不考虑轴心涡动 只计算该瞬态的稳定压力分布
end
end
%% 迭代过程计算
for i=2:n
for j=2:m
% PK(i,j)=(1-namda)*P(i,j)+namda*(ff(i,j)-(aa(i,j)*P(i-1,j)+bb(i,j)*P(i+1,j)+dd(i,j)*P(i,j-1)+ee(i,j)*P(i,j+1)))/cc(i,j); %加速收敛
PK(i,j)=(ff(i,j)-(aa(i,j)*P(i-1,j)+bb(i,j)*P(i+1,j)+dd(i,j)*P(i,j-1)+ee(i,j)*P(i,j+1)))/cc(i,j);
if PK(i,j)<0
PK(i,j)=0; %油膜破裂 置零
break;
end
end
end
%% 误差控制
sum1=0;
sum2=0;
for s=1:n+1
for t=1:m+1
sum1=sum1+abs((PK(s,t)-P(s,t)));
sum2=sum2+abs(P(s,t));
end
end
sum=sum1/sum2;
if sum<=ERR
break;
end
k=k+1
%% 遍历各处 i ,j
end
VV=6.*u.*omiga.*2.*pi./60.*R.^2./c.^2 %恢复成有量纲压力时的比例计算
% P=P.*VV; % 恢复成有量纲量
sitas=(0:n)*deltsita; %周向
Ls=(0:m)*(L/m); %轴向
[SITA,LL]=meshgrid(sitas,Ls);
mesh(SITA,LL,P')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 数值积分求等效力
Fx=0;
Fy=0;
for i=1:n+1
for j=1:m+1
Fx=Fx+P(i,j)*sin((i-1)*deltsita)*deltsita*deltL;
Fy=Fy-P(i,j)*cos((i-1)*deltsita)*deltsita*deltL;
end
end
fx=6.*u.*omiga*R.^4./c.^2*Fx
fy=6.*u.*omiga*R.^4./c.^2*Fy
f=sqrt(fx^2+fy^2)
theta=180/pi*atan(fy/fx)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 数值积分求等效力矩
Mx=0;
My=0;
for i=1:n+1
for j=1:m+1
Mx=Mx-P(i,j)*(deltL*(m/2+1-j))*cos((i-1)*deltsita)*deltsita*deltL;%P前面的符号将所有的力转换成沿x,y轴的正向;(m/2+1-j)的符号决定Z向坐标的正负
My=My+P(i,j)*(deltL*(j-m/2-1))*sin((i-1)*deltsita)*deltsita*deltL;
end
end
mx=6.*u.*omiga*R.^5./c.^2*Mx
my=6.*u.*omiga*R.^5./c.^2*My
m=sqrt(mx^2+my^2)
theta=180/pi*atan(my/mx)