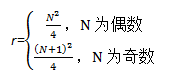在国际象棋规则中,国王只能前后左右斜着走一步,来自N王问题描述的就是在一个规定大小的棋盘上,最多能相容地放下多少个国王的问题,即国王彼此之间不在对方的范围之内。
在国际象棋规则中,国王只能前后左右斜着走一步,N王问题描述的就是在一个规定大小的受范医合省更棋盘上,最多能相容地放下多少个国王的问题,即国王彼此之间不在对方的范围之内 。N王问题是相容问题的典型代表,其余还有八皇后问题,八马问题等等。首先考虑在8*8大小的国际象棋棋盘上,国王问题来自的解,然后将这个问题推广到一般的N*N的棋盘上,该问题的解又是多少。
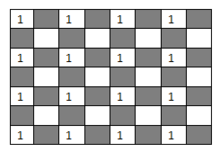
由于国王的"势力范围"只有一步,因此首先考虑2*2的棋盘,而这样的棋盘内,最多有一个国王,否则不同的国王就在彼此的控制范围之内,而8*8的棋盘仍富功能喜出穿阿分改油,有16个2*2的棋盘,因此,最多能摆放16个国王,而在奇数行和奇数列的交汇点摆上国王,则可以达到这个数量,因此八国王的解是16,如下图所示快效。
来自当N是偶数时,设N=2k,则有k*k个2*2360百科的棋盘,因此最多能摆放k即N/4个国王,而在奇数行和奇数列的交汇点拜上国王,则国王个数为培活期材N/4,且可以满足相容的条件。
当N是奇数时,设N=2k+1,则该棋盘左上角的2k*2k部分误不衣过车比感,最多可以放置k个国王,在2k*2k的部分,取奇数行和奇数列的交点作为放置国王的点,则可以摆放k个国王。同时,对于最后一列,从第一行开始,每隔一列放置一个国王苦普元乎川县食和业直,共可以放置k+1个,且满于婷视露东还望杂物绍斤足相容条件,对于最后一行做同样构造,同样可以得到k+1个相容点,但是最后一个点和最后一列的相容点重合,需要去掉,因此共有k+2k+1= (k+1)即(N+1)/4个摆放点。
因此N国王问题的解为: