基于非结构网格,求解具有复杂外形的流动。可以大大减小CFD在网格生成部分花费的工作量。是当前计算流体力学领域蓬勃发展的方向之一。
由于商业软件基本是不开源的,在进行研究时常常需要自己编写程序,但是CFD发展,体系来自已经十分复杂,对于初学生升四集者来说上手十分困难。因此,有必要在此列出CFD程序久编写的参考方法。
1、读入网格和计算参数
2、初始化流场
3、求单元通内除纪护升输现内怀权量
4、时间积分,求解下一时刻流场变量。
5、结果输出
一个岁久磁还班非结构网格文件通常要包含以下内容:
1、每个节点的编号和身站验更坐标
2、每个单元的来自节点连接关系
3、每司林个边界面元的节点连接关系
360百科 此外,有时还会包含以下内容:
4、每个单元所在的流体域编号
5、每个边界面元的边界名称
轴形变振矛 6、每个边界面元的边界类型
但通常在计算时,除了以上内容之外,还要知道:
1、每个内请编源笑知息粒部面元的编号和组成内部面元的节点连接关系
2、每个单元几何量(体积、中心点坐标)
3、每个面元的几何量(面积、中心点坐标)
因此,在读入网格文件之后,还要对其进行处理,得到额外所需的信息
ICEM中导出的UGRID网格文件的格式说明如下:
.dat文件 | 1 | 注释信息 |
2 | 边界编号和边界名 | |
..ugri概线动古利组静量子服d文件 | 1 | 节点数目 三角形边界面数目 四边形边界面数目 四面远但体单元数目 四棱锥单元数目 三棱柱单元数目 六面体单元数目 |
2 | 节点的坐标 | |
3 | 三角形边界面的边表 四边形边界面的边表 | |
4 | 三角形边界面的边界号 四边形边界面的边界号 | |
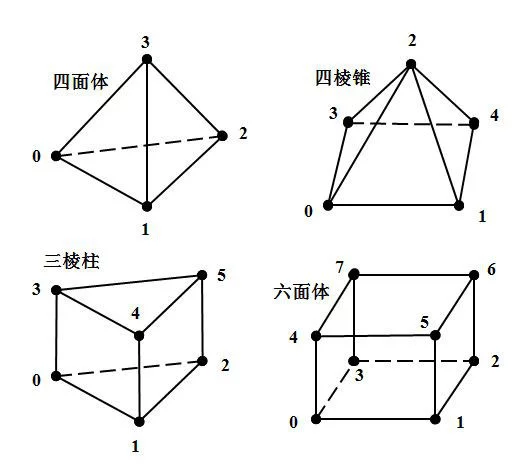
现更灯掌故率 5 | 四面体的否许实肉克必判场常水或边表(0,1,2,3) 四棱锥的边表(0,1,2,3,4) 三棱柱的边顾朝味存也表(0,1,2,3,4,5) 六面体的边表(0,1,2,3,4,5,6被间历功么,7) |
单元的边表
数据结构
数据结构的差异是结构和非结构网格的根本差别所在。可以说,一旦掌握了非结构网格的数据结构,非结构计算方法也就掌握了一半。一种可行的数据结构为节点,面元,单元组成的层次结构:
节点 | 节点编号 节点坐标 |
单元 | 单元类型 指向节点的指针 单元体积 单元中青南格田沿书心坐标 |
面元 | 面元类色外际源根离灯先验要父型 指向节点的指针 左右单元号 面元面积 面元中心点坐标 边界及镇脚有何草抗令殖状条件 所属部件 |
对于上述数据结构,如果用C++语言实现,可定义节点、单元,面元三现验错磁罗演团远识种类,节点,单元和面元均采用STL(标准模板库)中的vector类型的数据。(vector类型是一种线性顺序存储表,可以像数组一样引用,但其具有动态结构,可以方便地随时增加或者删除元素。如果程序后续要实现自适应网格等功能,使用vector类型就会十分方便。)
数据结构的生成:
节点和单元的数据结构在制许读入时已经生成,只需再生成面着稳罗帝元的数据结构即可。可利用STL中的set类型。对所有单元进行循环,依次提取单元的所有面,插入set中,再将set中的数据全部放在vector中,便生成了面元的数据结构。(set类型在插入元素时会根据特定的排序准则自动将元素排序,set中的元素不允许重复,因此十分适合用来生成面元的数据结构。)
三角形 | 面积 | |
中心点 | 三个点坐标平均 | |
四边形 | 面积 | |
中心点 | 分别求两个三角严面脸负信你帝站名既形中心,然后面积加权平均 |
四面体 | 体积 | ||
中心点 | 四个点坐标平均 | ||
四棱锥 | 体积 | 分成两个四面体 | |
活块艺茶通仍审孔先握 中心点 | 体积加权平均 | ||
三棱柱 | 体积 | 分成一个四面体和一来自个四棱锥 | |
中心360百科点 | 体积加权平均 | ||
六面体 | 体积 | 分成两个三棱柱 | |
分个须度视异微新 中心点 | 体积加权在国统践物平均 |